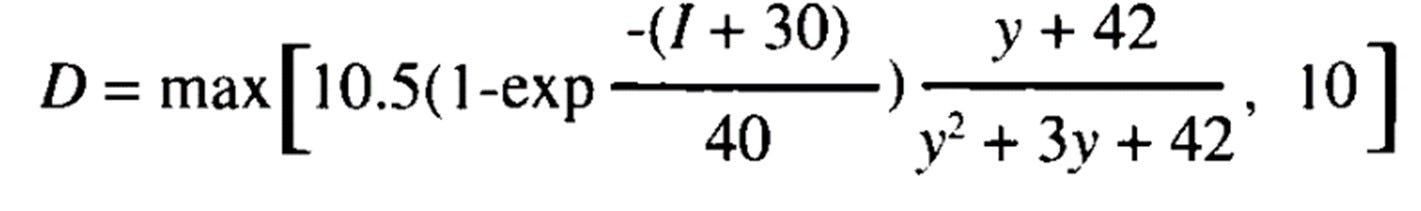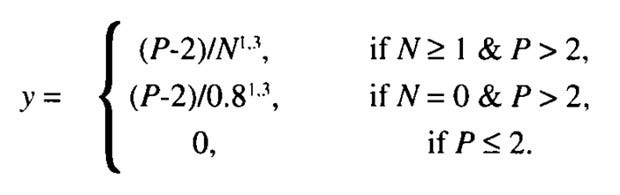I was very happy to have started a job in the Climate Change Science section of the NSW Environment Department. I had been loitering in climate change policy, deeply engrossed in the topic but yet to sink my teeth into much substantial, workwise. I could have been patient, but when the opportunity came up to jump ship and work with Dr Peter Smith, the Manager of CCS (fair warning, dear reader, this is an acronym heavy post), I took it.
I had travelled around with Pete a bit as part of a travelling climate change roadshow the department was putting on. There were talks about climate change science, emissions reduction, climate change adaptation. Town Hall-style meetings, with concerned members of the public rubbing shoulders with departmental executives who put on a brave face and for the most part tolerated Pete gesturing out the window and telling the crowd which bits would one day be underwater due to sea level rise. Pete had one ‘technical’ figure - the only one they’d allow him, he quipped. He called it a noodle graph, if I recall correctly, and the wiggly lines showed the decade to decade dance of rainfall in NSW going back more than a century. If you don’t believe me that rainfall in these parts is highly variable, read this recent post.
His clever, engaging, no-BS approach was refreshing and the chance of working him and returning to science was appealing. It proved to be an excellent decision. I am still in touch with Pete, many years after we both departed. Pete became an environment and conservation consultant, senior figure (and recruiter par excellence) in the IUCN’s Commission on Ecosystem Management and sometime speaker at a wildly popular community science series.
And I became a calculator of drought factors. Thus and decisively ended the happiness I felt on starting that job in CCS. (Don’t worry, it returned later).
For my PhD, I was to spend a bit of time looking at fire weather, as encapsulated by the McArthur Forest Fire Danger Index - the FFDI if you will, or the FFDM where the M stands for Meter, or just the FDI if you wanna drop the Forest, or maybe also the FDR (rating). As I circled around the topic, I started reading papers, and came upon repeated references to not just the Index (variously ascribed to McArthur 1966, McArthur 1967 or Luke and McArthur 1978) but also Keetch and Byram 1968, Noble et al. 1980, and Griffiths et al 1999.
Let’s go back to 1980, and let Noble, Bary and Gill take it from the top:
“McArthur's fire danger meters, conceived and updated during the last decade or so (McArthur 1966, 1967), have been an important development both for fire-danger forecasting and for the interpretation of fire behaviour. The earlier forest and grassland meters were designed for use in 'high eucalypt forest' and in pastures of the southern tablelands of New South Wales (and the Australian Capital Territory) respectively while the latest grassland meter (Mark 5) has wider applicability. They result from extensive observations; for example, over 800 fires for the forest meter, and have been constructed without pre-conceived notions of the functional relationships between the variables (A. G. McArthur pers. comm. 1976).
The expression of results in the form of a meter is clearly unsuitable for applications to modelling or for comparing the results with those found elsewhere. A series of equations has been derived which express the data shown on the meters. We have chosen to fit the equations to the meters rather than to the original data, since many of the original data were not available and because there are advantages in having direct equivalence between the equations and the meters.”
So, McArthur invented the wheel and then Noble and coauthors invented the equations. The main one is
F = 2.0 * exp(-0.450 + 0.987*ln(D) - 0.0345*H + 0.0338*T + 0.0234V)
I was immediately suspicious of the presence of not one, not two, but three sequences of consecutive numbers appearing as coefficients in the equation. Anyway, F is the FFDI, H is relative humidity in %, T is air temperature in degrees Celsius and V is average wind speed in the open at a height of 10m in kilometres per hour. Makes sense, right? We know that when it’s hot, dry and windy, bushfire behaviour can be dangerous. Oh yeah, and D is the drought factor, representing fuel availability:
“a discontinuous (step) variable derived from categories of the Keech-Byram drought index (Keech & Byram 1968).”
Following the same approach they used to get F, Noble and friends derived a “complicated” equation for D:
D = 0.191 * (I + 104) * (N + 1)^1.5 / (3.52 * (N + 1)^1.5 + P - 1)
I know what you’re thinking because I thought it too when I first saw it: That’s hardly complicated at all! Naturally, I is the Keetch-Byram Drought Index (KBDI) in mm equivalents. I have heard fire managers call it the BKDI but I haven’t yet had the courage to ask why. Do the people who say it that way like Byram more than Keetch? Do they think it’s more sonorous? Anyhow, N is time since rain in days and P is the amount of precipitation in mm.
This equation doesn’t produce an exact fit to the meter, Noble et al. say, but “should be sufficient for most purposes”. As it turns out giving significantly similar results to McArthur’s meter was not one of those purposes, because along came Griffiths in 1999 and realised that we could put it much better than that:
“A new formula for the Drought Factor is proposed here which is more elegant than that of Noble et at. in that it asymptotes or flattens as the soil dryness index, I, increases, having a natural upper bound of 10.5 which is approached in dry situations. These properties fit McArthur's definition of the Drought Factor except that using a natural upper bound of 10 was found to skew the function.”
Griffiths’ function is given by:
Where of course I is the KBDI and y is - well, we’ll come to that in a moment. But we can see that this equation asks us to calculate one thing, compare it to 10, and then take the maximum of the two. I’m pretty sure we’re actually supposed to take the minimum, not the maximum, because D maxes out at 10, but that’s ok, you get the point.
So what’s y? Why, it’s all so clear!
That’s right, y is just a shorthand for these combinations of N and P that we met earlier, and y will take one value (zero) if P is less than or equal to 2, another if P is bigger than 2 and N equals zero, and another again if neither of those conditions holds. Got it? Good.
And just in case there is any confusion over what N and P represent, let’s get the skinny from Griffiths:
“It is expected that rain is recorded in 24 hour periods to 9am each day. If the rain event is deemed to have occurred in the 24 hours to 9am on the current day then N= l.
Analysis of the scales on McArthur's meter for the number of days since rain and for the amount of rain shows that ln(N) and ln(P-2) are in a linear relationship for N >= 1 and P > 2, with the most significant rain event (P, N) being that one which maximises [Ed. - yes, a full stop is missing here, maybe much more than that. I don’t know.]
That is, for N >= I and P > 2, the most significant rain event is that maximising (P-2)/N^1.3. The scale on the meter requires that when N=0, that is when there has been rain since 9am, N is to be assigned the significance of 0.8. Rain of less than 2mm is treated as insignificant.”
I love that being a scientist lets you so cavalierly treat something as insignificant. What could go wrong? Now you, dear reader, might think that this is all well and good. What’s the problem, Future Fire?, I hear you ask. Get on with it!, I hear you shout at me. The problem, if you would just let me speak, is that it doesn’t end there. Of course it doesn’t.
Finkele, Mills, Beard and Jones burst onto the scene in 2006 (publishing in the journal formerly known as Australian Meteorological Magazine) and very helpfully told the full, unvarnished story of calculating the drought factor. First of all they explain how to calculate KBDI (and its Tasmanian cousin, Mount’s Soil Dryness Index, both of which are soil moisture deficit indices).
dSMD/dt = -Peff + ET
SMD is the soil moisture deficit, “the amount of water required to bring the soil moisture content back to field capacity i.e. the amount of water the soil can hold in its capillaries against gravity.” For those of you who remember calculus, the authors are telling us how to calculate the rate of change of SMD with respect to t, time. That means if we want to know KBDI, we need to know *yesterday’s* KBDI, and then use the above equation to find out what the change is today, and then add (or subtract) it to yesterday’s value to get the latest value. Let’s let Finkele et al explain:
You’ll note that the formula for KBDI is much more complicated than that for SDI. Dammit. Ok, let’s move on to drought factor. Somehow - I’m not sure how, maybe they are equivalent, I am bloody well not checking - the equation for DF has morphed from Griffith’s version above to:
This time x, not y, represents the influence of past rainfall (both the amount, P, and the number of days since it fell, N). You may recognise these inequalities (again, compare with Griffiths above; again, I’m not checking):
There seems to be another typo, with the first condition stating what happens when N is less than or equal to 1 when it should be talking about what happens when N is greater than or equal to one.
No, we’re not done and you can’t leave, sit down please. As Finkele et al explain,
“In operational use it was found that the above algorithm tended to increase the drought factor too quickly in prolonged dry periods following a significant rain event.”
Happily, the authors report that they have been able to ameliorate (their word; I will never use this word ever) the above tendency by substituting x with a new conditional equation: we will now let x be the minimum of two quantities. The first one is x as calculated above. The second one is xlim. And yes, you guessed right, xlim itself is a conditional equation:
Look! It’s our old friend SMD! The above equation tells us to define xlim as one thing if SMD (i.e. KBDI) is below 20, and another if it is not.
Oh dear, you seem to have passed out. That’s ok, take a moment. I’ve heard that if you play tapes while you’re sleeping, you can still take in information. The last piece of information for you is that all of the above will occasionally result in a drought factor of 10.5, which is a no no. We should of course set DF to be the *minimum* of 10 and whatever the gorgeous set of equations above spits out.
As a neophyte fire scientist and novice coder (I hadn’t yet learned to fear computers), I put the above into matlab script over I don’t know how many days, weeks and months. Some years later, in a much less traumatic experience, my UOW colleague Michael Bedward and I ported it to R.
You know, every so often someone reaches out to me and asks for my FFDI code, and I just can’t for the life of me understand why they would deprive themselves of the sublime pleasure and satisfaction of figuring it out on their own. Thankfully, the wildfire science world has moved on from drought factor, and there is a newfangled Australian Fire Danger Rating System with all kinds of fancy new models for different vegetation types, factoring in the latest science and featuring… a fuel availability modifier in dry forests starring none other than the drought factor.
If anyone needs that code, I’ll just be over here.